Langton's Ant is a 2D automaton which is Turing complete and also suitable for a simple mechanical implementation.
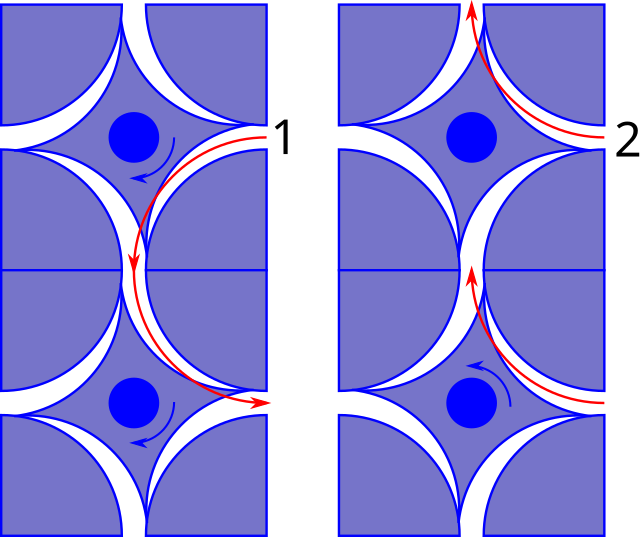
A star-shaped piece of plastic which can rotate about its centre is placed in the centre of each cell, and a circle of plastic placed in the corner of each cell blocks its movement and forms a thin channel between it and the star-shaped piece.

A small object entering from the right side (1) will be directed to the left and as it continues forward it will rotate the star-shaped piece to allow its exit at the base of the cell. The rotated star shape will direct the next object (2) which enters from the right upwards. The two rotation states of the star shape are analogous to the black and white state of a cell in Langton's ant. Given a large enough field of mechanical cells, all that is needed is a object which will continue to move forward in the channel to run Langton's ant.
Here's a video of a mechanical implementation. Skip on to about 4:20 to see it in action - before that I'm just explaining what Langton's ant is.
When I've made previous mechanical computers, I've avoided making memory out of custom-made pieces, because this is something which must be produced at large scale. For this reason the Turing machines I've made used ball bearings placed on standard steel grid as the memory. In this Langton's ant system, the memory is slightly more complicated to make, but the processing element is a simple as it could get.
Another advantage is that the proofs of universality of Langton's ant are much simpler and more compact (requiring fewer memory cells) than proofs which go via rule 110, such as the 5/2 Turing machine.
Complexity of Langton's Ant, University of Chile